"光量子系统”的力学公式推导杨-米尔斯场。
本文是在微观领域，用光量子系统的力学原理（物质守恒和牛顿定律）来推导杨-米尔斯场。说明粒子的非阿贝耳规范杨-米尔斯场本质上是微观领域里光量子系统的力学过程。对一个粒子，包括复合粒子来说，如果讨论的范围是离开粒子中心较远，则由于粒子的光量子系统的振荡而形成的对外的作用力场是电磁场，如果讨论的范围是离开粒子中心较近的范围，粒子的光量子系统的分布等位面是曲面，因此对于计算光量子系统的振荡而形成的对外的作用力场时，必须用“协变导数”来代替物质守恒和牛顿定律中的“导数”，从而得到杨-米尔斯场。本文是把四维规范场强，四维规范场势等概念都建立在光量子振荡能量、动量的力学过程的基础上。完全不采用经典的库仑定律，安培环路定律等宏观等实验定律，而是深入到粒子的光量子系统。进一步说明电磁力场、杨-米尔斯场场等都是光量子系统振荡的力学作用力场。进一步证明粒子是由光量子系统组成这一事实。进一步说明力学作用力场是是光量子系统振荡的力学作用力场，光量子系统振荡的力学过程是场统一的根本基础。
设粒子
中心为
，则可以建立直角坐标系为
。在分布等位曲面上，可以选择正交的主曲率线网及曲面法向，
，
，
为坐标参数，
为曲面法向。直角坐标系可以表示成：
。，，是曲线坐标，对同一个曲面是常数。曲线坐标通过旋转变换
可以与直
角坐标系对应。
在系里任取一小区域
，小区域内按照力学原理
， 
，（物质守恒和牛顿定律），
光量子系统的分布等位面是曲面，按照微分几何原理，考虑到坐标系的基矢在分布曲面上各点的方向是变化的，
必须用协变导数代替一
般导数。添上一些项的系数
并
把
改写成，恒等关系不变。
用协变导数代替一般导数后能动张量矩阵可以表达如下。
。
表示协变导数。
。这中间下标
对应直角坐标系的参数
,
对应于曲线坐标系的参数
，这些规定对下文也将如此使用。
为小区域内光量子受到的应力；
应该是周围空间对小区域体积元内光量子系统的作用力。由于光量子系统除了自身振荡外，没有
其它运动及受到其它力的作用，
即粒子对外的作用力，即电场力。
各向同性,在建立直角坐标系时可以选坐标轴为主轴。当
，
，当
，
。
于是在直角坐标系中的张量方程即为：
。
从直角坐标系到曲线坐标系
的变换是：
,
.
在直角坐标系里，光量子系统的张量方程是：
———
。
————
用
左乘两边，得到
和
都是曲度空间度量的，面应力应该与质量成正比，且同种材料，各向同性，
如果选择恰当的单位制。我们可以设定
，（常数选为
是为了与量子力学一致。）代入
即：
.
方程中的算子
，
，
，
作用在应力场的四维分量的同时也要作用在相应的基矢上。
。
是粒子
的态函数, 当
，
，
和
都对应与粒子的
光量子的密度，我们可以用
代替。从而这些得出：
。
在《光量子系统的对称方程》一文中我们已经得到状态方程：
，但考虑到坐标系的基矢在分布曲面上各点的方向是变化的，用协变导数代替一般导数，
由此得到：
. 其中
。
是磁量子数，相当于电荷电量
.上文已经得到：
———
用
左乘矩阵等式两边，得到：
.
定义
,即
,
,
.
即：
，
，把这些关系式代入
，并用
代入，
得到：
。
一个自由粒子具有一个四维的能动张量，同时它具有一个四维的态函数，
四维的能动张量与四维的态函数有相同的振动频率和位相，可以
认为
。“
”表示相似于。仿照上文用代替,可以认为：
。用
代替
,即
.
此式和上面的
式比较，
，
得：
………………（1）, 同理:
………………（2）,
………………（3）,
加上式
:
.
我们进行
的运算，
即：
即：
.
由矩阵关系式得到三维矢量
，
，
可以推得：
。
表示梯度。
已经定义，
推得
, 即.
,
,
。
,
得到:
………………
，
：，
得到:
参考，
得到：
-+
已经定义，
，
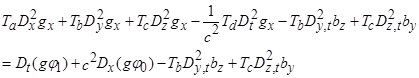即
.
同理：
.
加上等式
:
。
我们定义以上得到的四式 (11）——（14）为方程组
，参照方程组
建立矩阵关系式
:
假设
,则可以证明方程组与矩阵关系式等效。（见《附录》）
方程组中方程的第四个方程
式：
，
按上述的物质守恒定律：
，对于稳定系统，且周围没有其它外场的情况下
，
得到 
。
取齐次方程组
的特解，矩阵微分方程式
即成为矩阵微分方程式
：
,
定义矩阵关系式
，
这样可得到矩阵关系式
：
由上文得到：
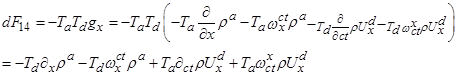
由上文得到
,
,
.
。
在用曲度度规度量的空间的直角坐标系中，任一点
， 
，
长度单位
的长度随它的位置而变化, 但它的方向没有改变。
。 
。
同样：
。
。
。
对照公式
和上面所述，
由此得出：
。
用曲度度规度量的空间中：
下标 “
”表示平度空间的量值。下标
“
”或省略下标的都是表示曲度空间的量值。
这中间为什么能取
呢，因为
只是
的一个起点，而点是曲面中任一点，又各向同性，在建立直角坐标系时可以选坐标轴为
主轴。在平度空间（即
空间）中可以认为相同，取什么值与问题并没有关系。
上文已经说明，各向同性,并且在建立直角坐标系时可以选坐标轴为主轴。这使得在平度空间（即空间）中有
，又各向同性, 
可示为常数，可令
。除了物理量单位外，可令
。
把已经得到的
，
，以及代入各式，得到：
,
。
。
从另一方面来看，在曲线坐标系中，
是四维张量场，
是张量场的分量，
它应该是一个矢量。
的基矢
的长度和方向 是随
的位置而变化。在坐标系,中必须用协变导数代替导数，必须求出相应于
的联络
。在光量子系统的分布曲面上，按微分几何：
,
。
从这些能得到联络：
,
,
。
矢量在直角坐标系中是
，
。
在曲线坐标系中是
，
。
从直角坐标系到曲线坐标系的变换是：。
,
,
。
。
。
对于速度从直角坐标系的
到曲线坐标系的
的变换是：
。
在直角坐标系中。
直角坐标系变换到曲线坐标系是： 
这一切说明：在曲面上如果采取直角坐标系则就有
在曲面上如果采取曲线参数坐标系，则就有
。
按微分几何，在直角坐标系里，曲率2型式
。
如果采取曲线参数坐标系
，
这些微分几何学的定义与我们所得到的结果除了因为采用了色动力学的
、
系数而相差外，其它完全一致。
在杨-米尔斯场中，分布曲面上，
即为规范场强
，而联络
即为规范场势
。曲面的曲率2
型式相应于规范场强
,这正是规范场论的一个重要观点。
回到上述的矩阵关系式
：
，
按照传统，所谓粒子
在处对外的场力，是把粒子作为整体对在点处的整体的外粒子的作用力。又认为粒子的电荷密度集中点，外粒子的电荷密度集中于点。对上述的矩阵关系式的右边，乘
和
，并对
区间进行二重体积分，
取时间周期的平均值：
.
为
的电荷量子数。
按照《光量子系统分析力学对电磁场应力张量的分析》一文所述，
，
，
即粒子在它周围处对外的作用力.是粒子在它周围点
处光量子系统对外周围处的作用力。对于静止或运动的粒子来说，由于光量子系统振荡（即电磁波）而引起的粒子与外界的作用力
即电磁场力。
即电力。
，
，
是点处对外的作用旋应力。这些论点在本文始终采用协变导数替代导数，对杨-米尔斯场的规范
场也同样适用。
同样对左式各项乘和，并对区间进行二重体积分，取时间周期的平均值，关系式中
、
、
经积分后用
表示，
，
即粒子在处对外作用电力场。
关系式中
、
、
经积分后用
表示，
应力的场强即磁感应场强， 磁感应场强
.
即粒子在处对外应力场。
对于本文始终采用协变导数替代导数，在粒子不受其它作用的情况下，即杨-米尔斯场的规范场强电场分量，即粒子在处杨-
米尔斯场的规范场的旋场分量。也可以这样说：对矩阵关系式
左边乘和，并对区间进行二重体积分，积分后
即表示粒子在处对外作用力场和旋应力场。
如果定义为粒子的电荷数，
，
，
，
分别表示在点的电流密度和电荷密度，
就可以得到矩阵关系式：
这就是规范场的爱因斯坦电磁张量矩阵，
与爱因斯坦电磁张量矩阵
实则上完全一致。
《附录》证明方程组与矩阵微分方程等价。
假设
, 我们能证明方程组与矩阵微分方程等价。
证明如下：
矩阵微分方程:
，
从矩阵微分方程,
能得到：
。
将
左乘
式两边，得到：
.
即
。
上文得到：
将
左乘式两边，上文有：,
即.,
,
。
,
,
。
得到：
.
即
,
同理：
.
加上等式
:
。
这四个方程式 (21)——（24）是矩阵关系式
经恒等变换而得到的结果， 而这四个方程式(21)——（24）是与方程式（11）——（14）
完全一致的，而四式 (11）——（14）即为方程组。故而矩阵关系式.
完全等价于方程组。证毕。
Introduction and Contents 引言和目录