破解广义相对论的曲度——度规变换函数(1)
爱因斯坦的广义相对论认为描述物理现象的“物理空间”，是应由空间物质的分布来决定的。这是对空间认识的一个革命性的飞跃。广义相对论认为在某种物理条件下，空间是曲度的，空间的表示应该用黎曼几何来代替欧几里德几何。在空间任意一个四维坐标系中，如果度规张量
是一个常数，曲度张量
这样的空间为平度空间。如果度规张量始终不是一个常数，曲度张量
，这样的空间为曲度空
间。与此相对应就有两种空间的两种度规（即度量单位），即平度度规和曲度度规。物理量的读数是和空间的度规有关。我们已经建立了两种
度规，用这两种度规（即度量单位）度量所得到的读数，分别相对应地描述了两个空间，即平度空间、曲度空间的物理量读数。
不过这些只不过是数学领域里的一种论述，我们应该从物理意义上来加以探讨。
物理空间并不是真空的空间，是一个物质空间，并且物质的分布并不是均匀的，物质分布是随空间位置的变化而变化。因此在建立两种度规
时，就必须考虑到物质的分布。
所谓“平度空间”即德波罗意空间，它实际上是一种假想的空间。“平度度规”即假定光速恒定为
而确定的度量单位。不论在真空中，或在
物质分布稠密处，都假定光速恒定为。在物质空间中如果假定光速恒定为，那么度量单位的长度就是随物质密度的变化而变化。“平度度
规”是可变的度量单位。在平度空间里，既然假定光速恒定为，那么物质的密度也将是假定不变的。若用平度度规（度量单位）来度量物质的密度也假定恒为
。下标f表示flat space,即平度空间。按照这种度规来度量，自由粒子将是一列平面波。量子力学的最基本原理，自由粒子的德波罗意假设就可以得到成立。在平度空间中用
作为可变的度量单位。用下标
表示用平度度规的度量单位来度量所得到的物理量的读数。如速度
，物质密度，……
所谓“曲度空间”即爱因斯坦空间，它是我们所处的空间，“曲度度规”即始终用“约定在任何相对运动的坐标系里，真空光速恒为, 借此
来定义各个坐标系的度量单位。”。借用这种度规（即度量单位），即使在介质里光速小于，甚至远小于，物质的密度很大等等的情况
下，度规的度量单位的长度将是始终不变的。在曲度空间里，光速是随物质密度变化而变化的，但度规的度量单位长度是始终不变的。我们常
用的“千克，米，秒”制单位即这种系列的单位。在曲度空间中用
作为统一不变的度量单位。用下标
表示用曲度度规的度量单位来度量
所得到的物理量的读数。下标c表示curvature space,即曲度空间。如速度
，物质密度
，……
“平度度规”和“曲度度规”都可以作为物理空间的同一物质的度量单位，它们之间必定存在着函数关系。我们用
来表示这种函数关
系。即
。读数曲
物理量的读数和度量单位的长度成反比关系，
按照上面所述的规定，有长度
，
，
，速度
，
，一个粒子的面密度
，
。一个粒子的体密
度
，
。
下文及网站的其它文章都将如此表示。
“平度空间”和“曲度空间”并不是两种不同的空间，只是用两种度规，即两种度量单位来度量物理量，得到同一空间的两种不同的读
数。并且这两种读数之间存在着函数关系。
现在，我们之所以这样来定义“平度空间”和“曲度空间”，是因为能与爱因斯坦的广义相对论的定义和内容取得一致。
无论用平度度量单位或是用曲度度量单位。真空光速恒为,
，即
。对一个粒子来说
，当
时，
，
。
。当一个粒子在复
合粒子之中或者在场中，度规变换函数
。下面文章将会对“
”作出详细的讨论。
如何按照上述的确定的两种度规的定义以及
的定义来导出呢？我们先来说明一个“独立性”原则。在场中有这样一个事实，在没有
发生裂变等的情况下，每个粒子都有各自固有的平度的度量单位和度规变换函数，在场中或者在其它粒子周围，每个粒子各自的固有
度量单位和将始终保持不变。在场中或者在其它粒子周围，若用粒子这固有的平度的度量单位和度规变换函数去度量,所得
到的结果是：这个粒子始终保持着原来孤立时的状态。不受场或另一个粒子存在的影响。那就是说在无裂变的情况下，每个粒子若用各自固
有的度量单位和去度量,它的光量子始终在各自原来孤立时态函数的等位面上分布着，运动着，光量子的分布仍保持不变。粒子保持
相对的独立性。然而两个粒子又可以看作一个复合粒子，两个粒子的光量子系统组成复合粒子的光量子系统。作为复合粒子的光量子，又都
将在复合粒子的等位面上分布着，运动着，在用复合粒子的和作度量单位的去度量，复合粒子在空间中形成一列平面波。
究竟如何按照上述的两种度规的定义以及的定义来导出呢？
如图
(1)
坐标系
简称为
系，
,
为两个自由粒子，
为它们的复合粒子。在系中，
为平面上任一点，也是,
这两个粒子光
量子的分布曲面上的任一个交点。点的坐标为
。
，点在
轴上，点的坐标为
。
,
在平面的
轴上，分别
与,
这两个粒子相对应。
,
在平面上。为第一个粒子光量子的分布曲面上过点的法线。为第二个粒子光量子的
分布曲面上过点的法线。
为第一个粒子等位面法截线的曲率半径。
为第二个粒子等位面法截线的曲率半径。这就是说,
分别为
二个粒子光量子的分布曲面的法截线的曲率中心。
，
,
即点为
的中点。
在平面上，
，
.
,
分别为光量子的两个分布等位面的法截线的切线。因此两个粒子的光量子，在点是沿着，
方向运动。（顺时针方向）。
在上，为复合粒子光量子的分布等位面过点的切线。作为复合粒子的光量子在点将沿的反方向运
动。在平面上作的垂线
，为复合粒子光量子的分布等位面的法线。
为复合粒子等位面法截线的曲率半径。
点不一定要
在
轴上。
,
,
,
,
。
，，
.
,
,
,
点在
轴上。当
时,
,
。
在三角型
中,
令
，
,
。
在三角形
中,令
，
,
。
， 。
第一个粒子的光量子 在方向上运动,
第二个粒子的光量子在
方向上运动,
复合粒子的光量子系统沿
方向运动，在点相碰以后，在
方向的动量之和等于0。
,
，在方向光量子的动量之和等于0,
.它们是在用曲度度规的度量单位度量的读数。
对于
,
中的光量子质点是在分布曲面的切面上，它们是等几率矢量，它们等几率地在各个方向运动的。受到方向限制.沿方向仅仅
只占一小部分。
以为中心,
为半径,通过
点作出了一球面
.
又以为顶点，为半径作一立体角元
,它和球面相交于
。
，
是矢径
。
是立体角元的顶角。 设交平面处的宽度为
。设
是沿平面方向运动的粒
子的光量子所占的体积元的表面积.
，
是球面中心到两端点的半径的夹角。
,
.
应是沿向运动的粒子的光量子的方向几率。沿方向运动的粒子的光
量子的方向几率是
。
同样，以
为中心，以
为半径通过点作一球面
,以为半径作一立体角元
。并使
。
是立体角元的顶角，
和球面
相交于
，交平面处的宽度为
。 
。设
是沿平面方向运动的粒子的光量子所占的体积元
的表面积.
，
是球面中心到两端的半径。
同理分析可得，沿方向运动的粒子的光量子的方向几率是
，
。。我们已经取，这样就有
.
相应的弦对
应的夹角
.
其次: 事实上在,
中的光量子并不能都被正向碰撞，仅仅在,
中的
,
这一小部分的两个粒子的光量子质点在
的时间间隔内被
正向碰撞。因此在
，
中两个粒子的光量子质点在的时间间隔沿方向正向碰撞几率分别是
，
。对
此分析如下：
如图2
.
设在点处，
，
分别为两个粒子的光量子质点的有效直径。
时刻有一对光量子质点在
处正向相碰，到
时刻，这对光量子质点各向前走过的路程，对第一个粒子的光量子质点走过的路程为
第
，对第二个粒子的光量子质点走过的路程为
。在
这段时间内，有效直径为的光量子质
点与有效直径为的光量子质点能发生正向碰撞。在这段时间内，能发生正向碰撞的有效面积
为
。同理，在这段时间内，有效直径为的光量子质点与这段距离内有效直径为
的光量子质点能发生正向碰撞的有效面积为
。而
，
， 
。由此得到
。对两个粒子来说
。正向碰撞几率分别为
，
。而，，说明对于在光量子分布曲面上，过点沿确定方
向的两个粒子的光量子质点在时间间隔里有相同的正向碰撞几率。
上面已经得到
。 考虑到方向几率
,
,并且还要考虑在，中在一定的时间隔里沿
一个确定的方向的两个粒子的光量子质点正向碰撞几率，分别是
，
。若在这个区域时硑撞次
，为一段时间内的硑撞次数。
则正向碰撞几率为
，
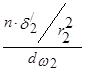。经过化简
.
，, 在体积元里光量子质点的数密度是
.
对于用曲度度
规度量
,
。 从这些可得到：
………（2）。
再回到图1来看，
,
,
,
,
。
点在的反向延长线上。
，，.
,
,
,
点在
轴上。当
时,
,
.在三角型
中,令，,
。
令
，
是等位面
的切綫，
。
.
,
.
,
.
由公式（2）
可得：
。
.
即
。
由此可得：
。 是增函数，取
。
.
. 取
，
对于在粒子等位面上通过点的每一法截线,曲度的转换函数是
。
是在粒子光量子分布曲面上的法截线的法曲率. 
。 取法截线法曲率的平均值,得到:
。
。 
, 
是分布曲面
,
曲线的主曲率。 因为粒子的分布曲面是光量子分布的等位面, 而分布的等位面是极小曲
面，
.这样能得到:
。
。
是在粒子微观物质分布曲面上点的高斯曲率.
,
。
对粒子光量子分布曲面上点的用平度度规和用曲度度规的度量的平均的转换函数是
。
。对所有的粒子,“
”是
一个常数,
它可能和普朗克常数有关。是积分常数，是由微分方程的初始条件决定的，下文将对此作详细讨论。
Introduction and Contents 引言和目录