1.对称的等几率矢量和破缺:
 坐标系
坐标系![]() 中, 以任意点
中, 以任意点![]() 为起点的矢量
为起点的矢量![]() ,在一段极短时间内,它的方向不断变化,并且任意一个方向都是等几率出现的,这样形成一个无穷多个矢量
,在一段极短时间内,它的方向不断变化,并且任意一个方向都是等几率出现的,这样形成一个无穷多个矢量![]() 的组合(N=1,
的组合(N=1,
2 ,……),定义这样的一组矢量![]() 为一个等几率矢量。
为一个等几率矢量。
当等几率矢量![]() (N=1,2
,……)在一定的时间间隔
(N=1,2
,……)在一定的时间间隔![]() 内,它们的长度相等,
内,它们的长度相等,
![]() , 则 定义这样的一组矢量
, 则 定义这样的一组矢量![]() 为对称的等几率矢量。
为对称的等几率矢量。
当等几率矢量![]() (N=1,2
,……)的长度不一定相等,在一定的时间间隔
(N=1,2
,……)的长度不一定相等,在一定的时间间隔![]() 内,
内,
![]() , 则定义这样的一组矢量
, 则定义这样的一组矢量![]() 为破缺的等几率矢量。
为破缺的等几率矢量。
须要说明的是,一定的时间间隔![]() 应该是一个很小、很小的时间隔,
应该是一个很小、很小的时间隔,![]() 。
。![]() 我们讨论的光量子系统有关的问题中,光量子的速度是每秒三十万公里,在粒子内部,光量子由于相互碰撞,速度的方向变化是非常、非常之快的。完全可以认为它们是一组等几率矢量
我们讨论的光量子系统有关的问题中,光量子的速度是每秒三十万公里,在粒子内部,光量子由于相互碰撞,速度的方向变化是非常、非常之快的。完全可以认为它们是一组等几率矢量
坐标系![]() 为静止系, 坐标系
为静止系, 坐标系![]() 相对
相对![]() 系静止。
系静止。![]() 系的一组对称的等几率矢量
系的一组对称的等几率矢量![]() ,
从静止系
,
从静止系![]() 来考察
来考察![]() ,
仍是对称的等几率矢量。 如果
,
仍是对称的等几率矢量。 如果
![]() 系相对
系相对![]() 系以
系以![]() 的速度运动,则
的速度运动,则![]() 系里的这组对称的等几率矢量,在
系里的这组对称的等几率矢量,在![]() 系考察时
系考察时![]() , 而等于一个方向与
, 而等于一个方向与![]() 一致或相反的矢量。这时就说
一致或相反的矢量。这时就说
![]() 系里的对称的等几率矢量,在
系里的对称的等几率矢量,在![]() 系里发生了破缺。这种破缺称之为相对运动破缺。
系里发生了破缺。这种破缺称之为相对运动破缺。
在物质分布不均匀的曲度空间中, (这里所指的曲度空间即爱因斯坦广义相对论中的曲度空间,是物质分布不均匀的空间。)
设坐标系![]()
为静止系,坐标系![]() 为
为![]() 系里的局部坐标系,
系里的局部坐标系, ![]() 系的一组对称的等几率矢量
系的一组对称的等几率矢量![]() ,
在
,
在![]() 系考察时, 因为各个方向的法曲率不同,
曲度不同,
系考察时, 因为各个方向的法曲率不同,
曲度不同,
![]() ,这组对称的等几率矢量
,这组对称的等几率矢量![]() 在
在![]() 系考察时发生破缺, 这种破缺称之为相对曲度破缺。
系考察时发生破缺, 这种破缺称之为相对曲度破缺。
在以静止系![]() 的原点为中心的库仑场中,一个电子绕中心旋转,角动量
的原点为中心的库仑场中,一个电子绕中心旋转,角动量![]() 的方向是等儿率出现的,
的方向是等儿率出现的,![]() ,是一组对称的等几率矢量。对
,是一组对称的等几率矢量。对
某些磁性物质,如果引入磁场![]() ,在磁场的曲度空间中
,在磁场的曲度空间中![]() ,
这时对称的等几率矢量发生了相对曲度破缺。
,
这时对称的等几率矢量发生了相对曲度破缺。
粒子的光量子质点在分布曲面切面的切线方向上运动着, 当分布曲面是球面时, 速度矢量是对称的等几率矢量. 当分布曲面不是球面时, 由
于各个方向的法曲率不同, 测度不同, 速度矢量不再是对称的等几率矢量, 而发生了相对曲度破缺.
粒子的同位旋角动量是粒子绕穿过这个粒子中心旋转的角动量. 旋转轴是空间的等几率矢量轴。角动量![]() 是空间的等几率矢量。 如果旋转
是空间的等几率矢量。 如果旋转
时![]() ,
, ![]() 是对称的等几率矢量.
如果粒子有运动速度
是对称的等几率矢量.
如果粒子有运动速度![]() ,或者周围存在磁场等等,
,或者周围存在磁场等等,![]() , 对称的等几率矢量发生破缺. 此时
, 对称的等几率矢量发生破缺. 此时
![]() 。 对一个粒子来说,
。 对一个粒子来说, ![]() 粒子对外呈现同位旋磁矩。
粒子对外呈现同位旋磁矩。
一个粒子包含着![]() 个光量子质点,(
个光量子质点,(![]() )。粒子光量子质点的自旋角动量是光量子质点绕穿过光量子质点自身的直线轴旋转的角动量. 旋
)。粒子光量子质点的自旋角动量是光量子质点绕穿过光量子质点自身的直线轴旋转的角动量. 旋
转轴是空间的等几率矢量轴。自旋角动量![]() 是空间的等几率矢量.
如果旋转时
是空间的等几率矢量.
如果旋转时![]() ,
, ![]() 是对称的等几率矢量.
如果旋转时
是对称的等几率矢量.
如果旋转时![]() ,
对称
,
对称
的等几率矢量发生破缺。
粒子的自旋角动量是粒子内部![]() 个光量子质点的自旋角动量之和,
个光量子质点的自旋角动量之和,![]() 。 对一个粒子来说,
。 对一个粒子来说, ![]() 即粒
即粒
子对外呈现自旋磁矩。式中![]() 表示粒子中光量子质点的总数。
表示粒子中光量子质点的总数。
2. 把实数、虚数、函数用等几率矢量来表示。
在复平面中![]() 轴为实轴,
轴为实轴,![]() 轴为虚轴。 但在空间我们可以用
轴为虚轴。 但在空间我们可以用![]() 轴表示一个实数,也可以用
轴表示一个实数,也可以用![]() 轴、
轴、![]() 轴表示一个实数,也可以在空间用任一矢量
轴表示一个实数,也可以在空间用任一矢量
![]() 为实轴表示一个实数。在空间中任一矢量
为实轴表示一个实数。在空间中任一矢量![]() 为实轴,
虚轴则分布在
为实轴,
虚轴则分布在![]() 轴的垂直平面上.
虚轴即此垂直平面上的等几率轴. 同样,在空间中任
轴的垂直平面上.
虚轴即此垂直平面上的等几率轴. 同样,在空间中任
一矢量![]() 为虚轴, 实轴则分布在
为虚轴, 实轴则分布在![]() 轴的垂直平面上. 实轴即此垂直平面上的等几率轴。只有把设定的坐标轴看作等几率轴,引入等几率轴、
轴的垂直平面上. 实轴即此垂直平面上的等几率轴。只有把设定的坐标轴看作等几率轴,引入等几率轴、
等几率矢量的概念,才能完整地表示出复空间的实体。譬如:
一个电子绕库仑埸中心旋转, 电子的态函数![]() 的图象是球贝塞尔函数,而电子的实际轨迹是环绕中心的电子云。只有把坐标系
的图象是球贝塞尔函数,而电子的实际轨迹是环绕中心的电子云。只有把坐标系![]() 的
的
一个轴,如![]() 轴看作等几率矢量轴,把
轴看作等几率矢量轴,把![]() 轴看作空间的等几率矢量而建立起的坐标系及图象,这样去认识它,使球贝塞尔函数立体化,才能反
轴看作空间的等几率矢量而建立起的坐标系及图象,这样去认识它,使球贝塞尔函数立体化,才能反
映电子运动和分布的实际轨迹。![]() 对于函数,我们往往必须选用等几率轴来建立起坐标系及它的图象的概念,才能反映质点运动和分布的实际
对于函数,我们往往必须选用等几率轴来建立起坐标系及它的图象的概念,才能反映质点运动和分布的实际
轨迹。
纯数学的空间,它是脱离参照物的空间,它的基的方向是任选的,可以把它看作是一组等几率矢量,或者说它的主轴是等几率轴。如果引入
某个参照物,如一条有方向的直线,或某些物理条件(如场),这样的空间是一个物理空间。 物理空间的基或者主轴,不再是等几率矢量,
而赋予确定的方向,物理空间是一个有确定方向的空间,它是纯数学空间的一种破缺。
3.对称等几率矢量的矢量化。
对于一组对称的等几率矢量,我们往往把它分成正负两组矢量。这就如同数轴一样。任一数轴确定原点![]() 以后,轴上
以后,轴上![]() 点的右边为正,左边
点的右边为正,左边
为负。对于对称的等几率矢量,同样也是这样,确定原点![]() 和过
和过![]() 点的平面以后,平面的上半空间的等几率矢量为正,下半空间为负。(或与
点的平面以后,平面的上半空间的等几率矢量为正,下半空间为负。(或与
此相反)。以运动的质点(光量子)为例,运动方向指向平面,在平面上方的质点为入射光量子。而运动方向离开平面,在平面下方的质点
为出射光量子。由于从能量和动量来考察,它们对外的作用是不同的,是应该分别加以计算。射向平面,运动方向在平面上方(![]() )的
)的
质点是输入能量或动量。射离平面,运动方向在平面下方(![]() )的质点是输出能量或动量。统计它们振动的能量和动量时,只须取半个
)的质点是输出能量或动量。统计它们振动的能量和动量时,只须取半个
空间。再以光量子自旋为例,![]() 的方向指向平面的上半空间的光量子自旋角动量为正,
的方向指向平面的上半空间的光量子自旋角动量为正,![]() 的方向指向平面的下半空间的光量子自旋角动量为
的方向指向平面的下半空间的光量子自旋角动量为
负。把一组对称的等几率矢量分成了方向相反的两个部分,即对对称的等几率分成(![]() )和(
)和(![]() )两个部分进行积分,形成两个矢
)两个部分进行积分,形成两个矢
量,并只取其中一个矢量,这样的运算定义为对称等几率矢量的矢量化。
然而,分成两个部分进行积分,两个部分的分界面是可以按照实际情况取的。往往取某个切面的方向。积分的0轴的方向是与积分求和范围的分界面的垂直方向。另一种方式是积分的0轴的方向可以按照实际情况取的,可以是平行另外一个已知矢量的方向,或平行于另一组对称等几率矢量的矢量化后的矢量方向,此时积分求和范围的分界面的方向是与积分0轴的垂直方向,按照后一种方法,这样两组对称等几率矢量,它们矢量化后的矢量方向可以同步相同。这就是所谓两个矢量实现了“几率同步”。“几率同步”是我们这个课目的一个重要课题。
任一个光量子的运动方向,动量方向是任意的,是一组对称的等几率矢量。但当两个光量子碰撞时,须要实现对称等几率矢量的矢量化,一个光量子为入射粒子,另一个光量子为出射粒子。对每个光量子矢量化时,两个光量子碰撞时的动量的积分界面是与碰撞方向的垂直方向,积分的0轴的方向是碰撞方向。有时候往往把两个光量子碰撞的方向总取作x轴的方向或某个曲面的切线方向。
不仅两个对称等几率矢量矢量化后的矢量方向可以同步相同。若干个,甚至一群,一大群对称等几率矢量矢量化后的矢量方向可以分别同步
相同。以粒子的自旋为例,一个粒子包含![]() 个光量子质点(
个光量子质点(![]() ),而每个光量子质点的自旋角动量是绕穿过各个光量子质点自身的等几率
),而每个光量子质点的自旋角动量是绕穿过各个光量子质点自身的等几率
直线轴旋转的对称等几率矢量。每个光量子质点的自旋角动量![]() 也是对称等几率矢量,
也是对称等几率矢量,![]() 个微观质点的对称等几率矢量经矢量化后的矢量方
个微观质点的对称等几率矢量经矢量化后的矢量方
向都可以认为同步相同,整个粒子的自旋角动量![]() 可以认为是一致的。也可以认为整个粒子的自旋角动量
可以认为是一致的。也可以认为整个粒子的自旋角动量![]() 是某个特定的方向。
是某个特定的方向。
对称等几率矢量的矢量化与矩阵中的列矩阵或矩阵有相似之处,它们可以灵活地选择坐标系主轴,然而能够表示粒子的某些矢量或某些物理
特性。![]() 矩阵中的列矩阵或矩阵往往可以作为对称等几率矢量的矢量化的一个表示。量子力学中为什么常可以用矩阵来表示物理量,实则上
矩阵中的列矩阵或矩阵往往可以作为对称等几率矢量的矢量化的一个表示。量子力学中为什么常可以用矩阵来表示物理量,实则上
就是用矩阵来表示同步的对称等几率矢量,这就是其中的一个原因。
须要说明的是在讨论几率同步时,须要考虑到统计的概念。上文已经说明,如果等几率矢量![]() 是对称的等几率矢量, 则在时间间隔
是对称的等几率矢量, 则在时间间隔![]() 内
内![]() 。同样在讨论对称等几率矢量
。同样在讨论对称等几率矢量![]() 是对称等几率矢量时,也须要在一定的时间间隔
是对称等几率矢量时,也须要在一定的时间间隔![]() 内
内![]() 。并且必须
。并且必须![]() 。当它们都是对称等几
。当它们都是对称等几
率矢量时,方可以讨论它们的几率同步问题。
4.对称等几率矢量破缺以后的矢量化:
对称等几率矢量发生破缺,破缺后形成一个特殊的方向的矢量。这个特殊的方向一般来说即破缺的方向。
坐标系![]() 相对坐标系
相对坐标系![]() 沿
沿![]() 轴方向相对运动,相对运动速度为
轴方向相对运动,相对运动速度为![]() ,
,![]() 的方向即
的方向即![]() 轴方向。坐标系
轴方向。坐标系![]() 中一等几率速度矢量
中一等几率速度矢量![]() 相对
相对![]() 系为对称的
系为对称的
等几率矢量。但从![]() 系考察时,等几率速度矢量
系考察时,等几率速度矢量![]() 发生了破缺。
发生了破缺。
现在对此作进一步的分析、证明。
质点![]() 相对坐标系
相对坐标系![]() 速度为
速度为![]() ,
,![]() 在坐标系
在坐标系![]() 是一组对称的等几率矢量。质点在坐标系
是一组对称的等几率矢量。质点在坐标系![]() 的坐标是
的坐标是![]() ,
,![]() ,
,![]() 。质点在坐标系
。质点在坐标系![]() 的坐标是
的坐标是
![]() ,
,![]() ,
,![]() 。
。
 设
设![]() 与
与![]() 轴方向的夹角为
轴方向的夹角为![]() 。平面
。平面![]()
![]() ,在的
,在的![]() 平面上的投影与
平面上的投影与![]() 轴方向的夹
轴方向的夹
角为![]() 。
。![]() ,
,![]() ,
,![]() 。
。 ![]() 坐标系
坐标系![]() 相对坐标系
相对坐标系![]() 沿
沿![]() 轴方向
轴方向
以速度![]() 运动,按照洛仑兹变换,从
运动,按照洛仑兹变换,从![]() 系考察时,质点的速度
系考察时,质点的速度 ,
,
 ,
, 。它们是等几率
。它们是等几率
矢量。对等几率矢量求和![]() ,
,![]() ,
,![]() 。当
。当![]() 取相同值,
取相同值,![]() 从
从![]() 积分时,
积分时,![]() ,
,![]() 。
。
 ,
, ![]() ,
, ;
;
![]() ,
, ,
,
![]() ,令
,令
![]() ,
, 。
。
![]() ,
,![]() ,计算可得:
,计算可得:
 ,
,
![]()
![]() ,同时
,同时
![]() ,
,![]() 。这说明经过洛仑兹变换和等几率矢量矢量化的统计后,所得到的矢量
。这说明经过洛仑兹变换和等几率矢量矢量化的统计后,所得到的矢量![]() 的方向仍是沿
的方向仍是沿![]() 轴方
轴方
向。
由此可以得知,从当坐标系![]() 相对于坐标系
相对于坐标系![]() 以
以![]() 的速度运动,从坐标系
的速度运动,从坐标系![]() 考察,坐标系
考察,坐标系![]() 中的一个对称的等几率速度矢量经过洛仑兹变换
中的一个对称的等几率速度矢量经过洛仑兹变换
和等几率矢量矢量化的统计,此对称的等几率速度矢量发生破缺,形成一个方向与坐标系![]() 相对于坐标系
相对于坐标系![]() 的运动方向
的运动方向![]() 相同的速度矢量。
相同的速度矢量。
如果把粒子的速度矢量改为粒子的振动速度矢量也可以得到同样的结果。
现在再考虑粒子旋转的情况:
设坐标系![]() 为静止系,粒子
为静止系,粒子![]() 的中心位于
的中心位于![]() 点。
点。![]() 为粒子
为粒子![]() 中任意光量子分布曲面上的一个光量子质点,过
中任意光量子分布曲面上的一个光量子质点,过![]()
点作坐标系![]() ,它的
,它的![]() 軕与坐标系
軕与坐标系![]() 的
的![]() 轴平行,坐标系
轴平行,坐标系![]() 相对坐标系
相对坐标系![]() 以旋转角速度为
以旋转角速度为![]() 旋转,为了说明简单,假设
旋转,为了说明简单,假设
![]() 的方向为
的方向为![]() 方向,
方向,![]() 为光子的自旋角速度。
为光子的自旋角速度。![]() 小于
小于![]() 。设坐标系
。设坐标系![]() 中任一光量子质点
中任一光量子质点![]() 以
以![]() 自旋,
自旋,![]() 是对称等几率矢量。设
是对称等几率矢量。设
![]() 与
与
![]() 轴方向的夹角为
轴方向的夹角为![]() ,
, ![]() 在的
在的![]() 平面上的投影与
平面上的投影与![]() 轴方向的夹角为
轴方向的夹角为![]() ,
,
![]() 在坐标系
在坐标系
![]() 的三个轴上的分量为
的三个轴上的分量为![]() 、
、![]() ,
,
![]() 。
。![]() ,
, ![]() ,
,![]() 。
。
![]() 坐标系
坐标系![]() 相对坐标系
相对坐标系![]() 存在旋转角速度为
存在旋转角速度为![]() ,
,![]()
![]() 的方向为
的方向为![]() 方向。按照旋转运动的洛仑兹变换,若从坐标系
方向。按照旋转运动的洛仑兹变换,若从坐标系![]() 上考察,则
上考察,则
 ,
,
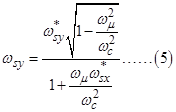 。
。 。
。
![]() 、
、![]() 、
、![]() 、
、![]() 为从坐标系
为从坐标系![]() 上考察时微观质点
上考察时微观质点![]() 的自旋旋转角速度和它的分量。若将自旋变量变更为平动变量,则式
的自旋旋转角速度和它的分量。若将自旋变量变更为平动变量,则式![]() 、
、![]() 、
、![]() 与上文
与上文
讨论质点平动时的![]() 、
、![]() 、
、![]() 对应式完全相似,经过完全类似于上文1,2,3的计算,按照等几率矢量矢量化的统计原理,得到的一个破缺
对应式完全相似,经过完全类似于上文1,2,3的计算,按照等几率矢量矢量化的统计原理,得到的一个破缺
矢量,它可以看成与坐标系![]() 相对坐标系
相对坐标系![]() 旋转速度方向一致的一个定向的旋转的角速度矢量。从
这个结论又可以得出如下的结论:
旋转速度方向一致的一个定向的旋转的角速度矢量。从
这个结论又可以得出如下的结论:
坐标系![]() 相对于坐标系
相对于坐标系![]() 以
以![]() 的旋转速度运动,从坐标系
的旋转速度运动,从坐标系![]() 考察,坐标系
考察,坐标系![]() 中的一个对称的等几率旋转速度矢量经过洛仑兹变换和等几率矢
中的一个对称的等几率旋转速度矢量经过洛仑兹变换和等几率矢
量矢量化的统计,此对称的等几率旋转速度矢量发生破缺,形成一个方向与坐标系![]() 相对于坐标系
相对于坐标系![]() 的旋转速度方向
的旋转速度方向![]() 相同的旋转速度矢
相同的旋转速度矢
量。
如果把粒子的自旋角速度矢量改为粒子的自旋振动速度矢量也可以得到同样的结果。
Introduction and Contents 引言和目录